lookigroups.blogg.se - Cellprofiler curved chord length

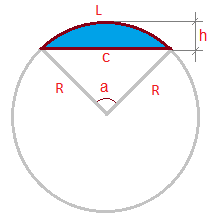
Chord Length from Arc and Radius - This computes the length of the chord based on the length of arc and the radius of the circle.Radius from Chord- This computes the radius of a circle based on the length of a chord and the chord's center height.

Radius from Area - This computes the radius of a circle given the area.Circumference from Area - This computes the circumference of a circle given the area.Radius from Circumference - This computes the radius of a circle given the circumference.Circle around a Triangle - This computes the radius of a circle that circumscribes a triangle given the length of the three sides ( a,b,c) of the triangle.Circle within a Triangle - This computes the radius of a circle inscribed within a triangle given the length of the three sides ( a,b,c) of the triangle.Arc Lengths - This computes the length of a cord segment (arc length) on a circle given the radius (r) and angle ( Θ).Circumference - This computes the circumference of a circle given the radius ( C = 2 π r).Radius - Center to a Point - This computes the radius of a circle given the center point ( h,k) and any other point ( x,y) on the circle.Area of Annulus- This computes the area of an annulus (ring) given the inner radius ( r) and outer radius ( R).Sector Area f(r,Θ)- This computes the area of a sector (pie slice) of a circle given the radius ( r) and angle ( Θ).

Line String The B-spline curve is dropped. Facet To : Sets the element type to which the selected B-spline curve is converted. Equal Parameter Length The B-spline curve is evaluated evenly in the parameter space by the Number value. It is based on using the radius point of the curve as the reference point. Chord Height The maximum chord height for all of the line segments is less than the Chord Height. len., ch) Delta () The angular change along a curve, from the beginning of the curve to the end of a curve.

Segment Area f(r,h) - This computes the area of an arc segment of a circle given radius ( r) and the depth ( h) into the circle. Chord Length The straight-line distance from one end of a curve to the other end of a curve.

Segment Area f(r,θ) - This computes the area of an arc segment of a circle given the radius ( r) and angle ( θ).

Circle Area - This computes the area of a circle given the radius (A = π r 2).

The length of the chord (d) is the distance between two points on a circle. The formula for the length of a chord is: However, this can be automatically converted to other length units via the pull-down menu. INSTRUCTIONS: Choose units and enter the following:Ĭhord of a Circle (d): The calculator compute the length of the chord ( d) in meters. Therefore, the chord length will be 11.The Chord of a Circle calculator computes the length of a chord ( d) on a circle based on the radius ( r) of the circle and the length of the arc ( a).

Chord Length Using Perpendicular Distance from the Centre of the circle: \(C_\\ = 2 \times 5.744\\\).

Therefore, the two basic formulas for finding the length of the chord of a circle are as follows Thus using Pythagoras theorem, we may find the length of the chord CD easily. It is due to the fact that perpendicular drawn from centre O on chord CD will be the bisector of CD. We may also calculate the chord length if we know both the radius and the length of the right bisector. We may determine the length of the chord from the length of the radius and the angle made by the lines connecting the circle’s centre to the two ends of the chord CD.

the longest chord, ‘OE’ will be the radius of the circle and line CD represents a chord of the circle, whereas curve CD will be the arc. In the given circle having ‘O’ as the centre, AB represents the diameter of the circle i.e. The same two points are connected by the curve in the form of the corresponding arc in the circle. 3 Solved Examples for Chord Length Formula What is a Chord in a Circle?Ī chord is the line segment in a circle, which connects any two points on the circumference of the circle.